BMDev 6: Populations
How colliding constraints lead to creation
Playing a game and designing it have a surprisingly large overlap in requisite thinking. The areas they don’t hold in common is where serious design work must be undertaken.
When presented with a complex game we intend to master, we approach the game in a 3-part cycle1: we read the rules, play them out as we understand them, and evaluate the achieved outcomes to refine our understanding of the rules (which we read more carefully, and so on). But when designing a game, this cycle takes on higher dimensions.
At each step of the cycle, a player should ideally charge forth with confidence! The player doesn’t have the authority to change the rules; he is implicitly relying on their correctness! Any mistakes he makes will be in either misunderstanding the rules (lack of knowledge) or not fully commanding their implications in gameplay (lack of skill). But as designers, we can intervene and question and re-examine at every step of the cycle; this is a terrible time-destroying evil to be avoided!
There are techniques to deal with this problem, depending on what is being examined. In this writeup, we will uncover how identifying a single number allowed us to “automate” the design of an entire game system.
Tremendous thanks to the warriors who support this publication! The bold-hearted fanatics among you who have supported us directly (through paid subscription here on Substack) have undeniably hastened the development of BMD—and the destruction of our enemies!
The rulebook is coming along at pace with daily content updates, and the goal is to straight-line towards playtesting. The first prototype to make it into your hands may not have all the bells and whistles, but it will put more than enough lead down-range.
More direct support here means a playable rulebook sooner! And command has been plotting ways (advanced editions etc.) to reward our finest fighters. This game is dedicated to men like you—those with taste, intelligence, and a bold vision of a future dominated by TTRPG Supremacy!
Simulationist Core
The secret to this power is having simulationism2 as the logical glue binding game mechanics together. The conceptual design of the game—the relation of its main ideas with each other—is a complex web informed by intent, aesthetics, gamesmanship sense, and other things. But simulationism is the tool that keeps the tables and dice mechanics in sync with Second-World expectations and intuitions that players have—it’s a tool that helps efficiently convey a realizable gameworld3.
When we ran into logical inconsistencies with questions about the populations of settlements in BMD, it was suspected that an underlying simulationist system would make these issues disappear. The true source of the problem was difficult to find, but the solution eventually presented itself from an unexpected direction involving a completely different question!
Transit and Travel
Our population numbers—simply put, the number of people that live in an area—create contradictions, but let’s ignore that for a moment. In BMD there is a systematic way to play out the various kinds of transit and travel.
If we are in star system A and need to get to star system B, we will just plot a course and wait for our ship to arrive; there’s more to it than that, but this is the essential description.
If we arrived in star system B and need to get to a particular planet, we again plot a course and wait. With typical starship technology, it takes 24 hours to get from a specific point in a star system to another specific point—exceptional cases notwithstanding.
We’re in orbit of the desired planet and want to land in a particular settlement. Making landfall from orbit takes somewhere between minutes and hours, depending on technologies and circumstances.
Now we’ve landed in a settlement4. It is divided into districts. Simply put, moving from one district to another takes a certain amount of time.
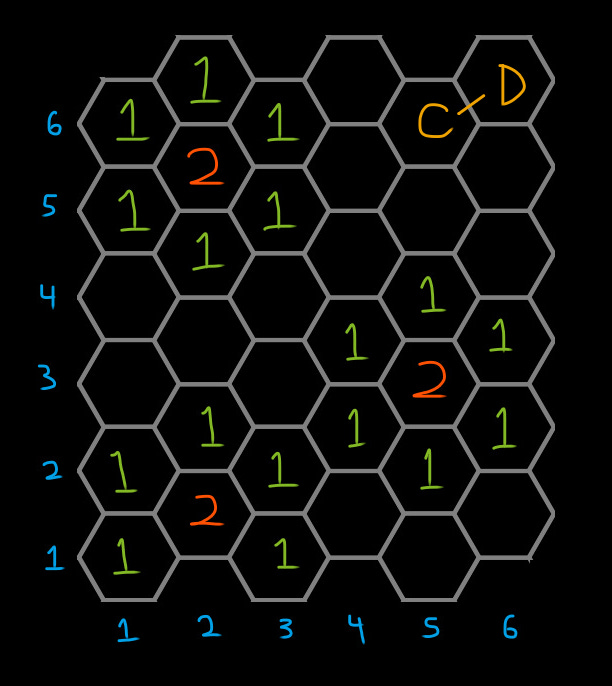
Consider the map of the settlement above. If we have forces at C (5,6) and want to move to D (6,6), that’s a move from one district to an adjacent one. Districts serve to split up different areas of a settlement logically but also act as gameplay boundaries. When moving from one district to another, we check for encounters5. If an encounter occurs, we can afterward describe where it occurred—which district and what the terrain was like and so on.
All good and well—but how long does it take? Strangely, the answer to this question leads directly to the basis of the whole population system!
Implications of Travel Time
Consider the assertion that vehicles take 4 hours to move districts whereas troops on foot take 24 hours. If we assume these are facts set in stone, the scope of implications that follow is astonishing.
Assumption 1: A vehicle takes 4 hours to cross from one district to the next.
For this to be interpreted charitably, we imagine this time as some kind of aggregate of averages and conceptualize the crossing happening generally from the center of one district to the center of another. For geometric reasons, there is a whole class of equivalent distances behind this reasoning, and we hold to this slight abstraction.
Since this trip is imagined as an aggregate, our vehicle will have some average speed—is it 5mph or 100mph? Assuming land travel—looking at APCs, tanks, and similar land vehicles—we can see top speeds of between 60 and 100mph in the main. Top speeds require ideal conditions, and columns cannot move in ideal conditions without roads and so on. Presuming that our men are moving between districts using roads when possible but avoiding them when prudent, it is reasonable to establish the average vehicle speed as 20mph.
Assumption 2: Vehicles move at an average of 20mph.
Note that Assumptions 1 and 2 combine to create a clear conclusion. Moving at 20mph for 4 hours puts us at a total average distance of 80 miles.
Fact 1: District travel length ‘S’ is, on average, 80 miles.
If ‘S’ is 80 miles, it means that the “size” of the hex is 80 miles due to the equivalent distances logic above. To simplify the math and presentation, we’ll consider the case of square districts rather than hexagonal districts; the differences are minor, and it will illustrate the principle more simply.
An 80mi × 80mi square has 6400 square miles of area. Our 80mi × 80mi square can be split into 100 8mi × 8mi blocks. This leaves us a square district with ten blocks by ten blocks, each of 8mi × 8mi. We’ll come back to this point later.
Fact 2: Our districts are, on average, 6400 square miles.
Studying Up on Population Density
Considering that settlement Sizes go from 3 to 7, meaning a 3×3 grid up to a 7×7 grid, we do some research on this size to get some impressions. A 3×3 grid is 240mi × 240mi.
Keep reading with a 7-day free trial
Subscribe to Primeval Patterns to keep reading this post and get 7 days of free access to the full post archives.